Exponentielles Wachstum

Von exponentiellem Wachstum spricht man dann, wenn sich etwas jeden Tag mit einem festen Faktor vervielfacht. Also beispielsweise dann, wenn sich etwas jeden Tag verdoppelt. Dann beträgt der Faktor 2.

Nehmen wir die Verbreitung einer ansteckenden Krankheit als Beispiel: Da wir eine ausgedachte Krankheit betrachen, müssen wir Annahmen machen, insbesondere, wie viele Personen von einem Infizierten pro Tag angesteckt werden. Machen wir hier die Annahme, dass jeder Infiziert pro Tag eine weitere Person ansteckt. Starten wir mit einem Infizierten, dann haben wir nach einem Tag zwei Infizierte. Nach zwei Tagen sind es schon vier, da jeder der zwei einen weiteren infiziert. Weiter geht es mit acht nach drei, 16 nach vier und 32 nach fünf Tagen. Nach 14 Tagen sind es 16.384 Infizierte, wenn wir anehmen, dass niemand in dieser Zeit verstorben oder genesen ist.

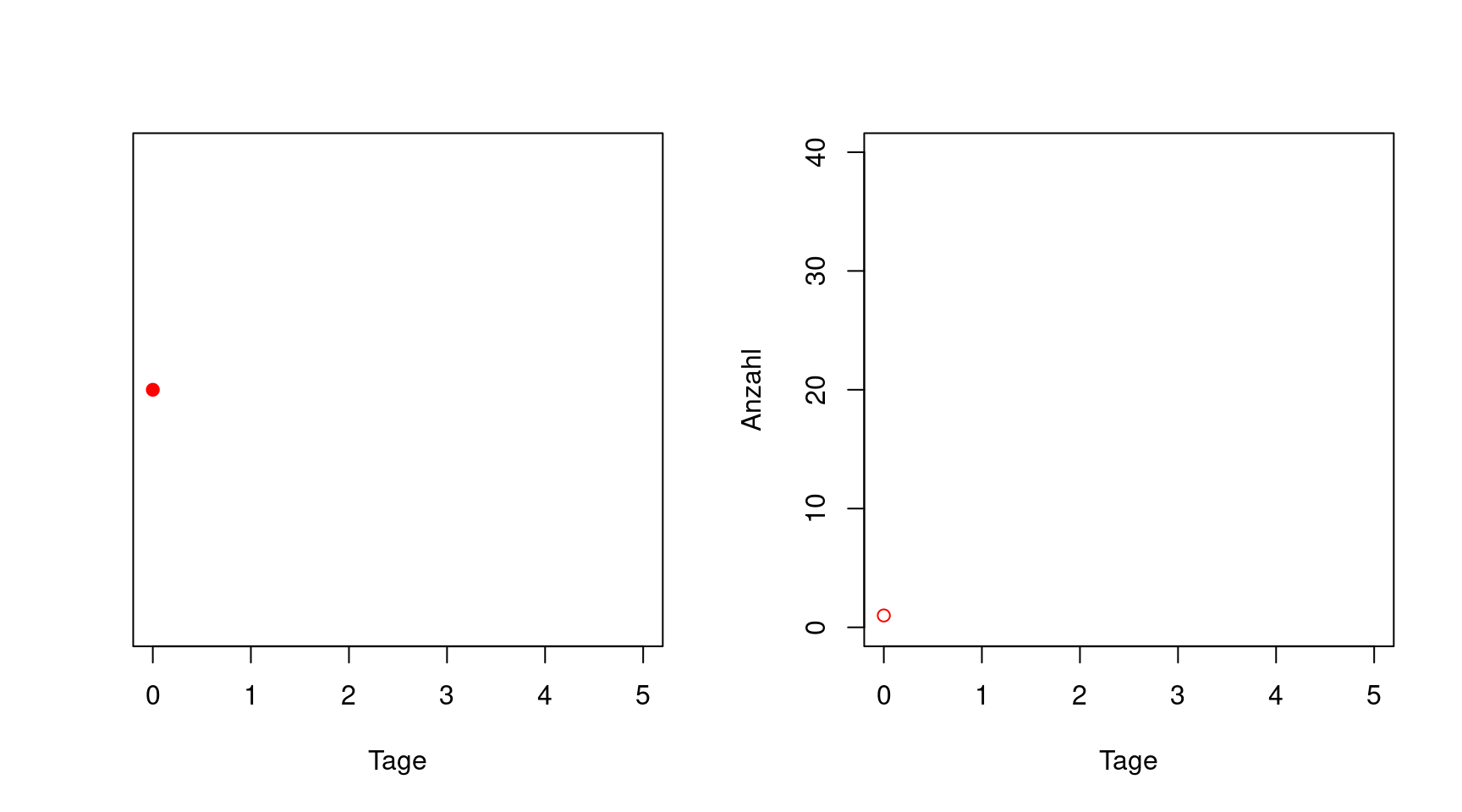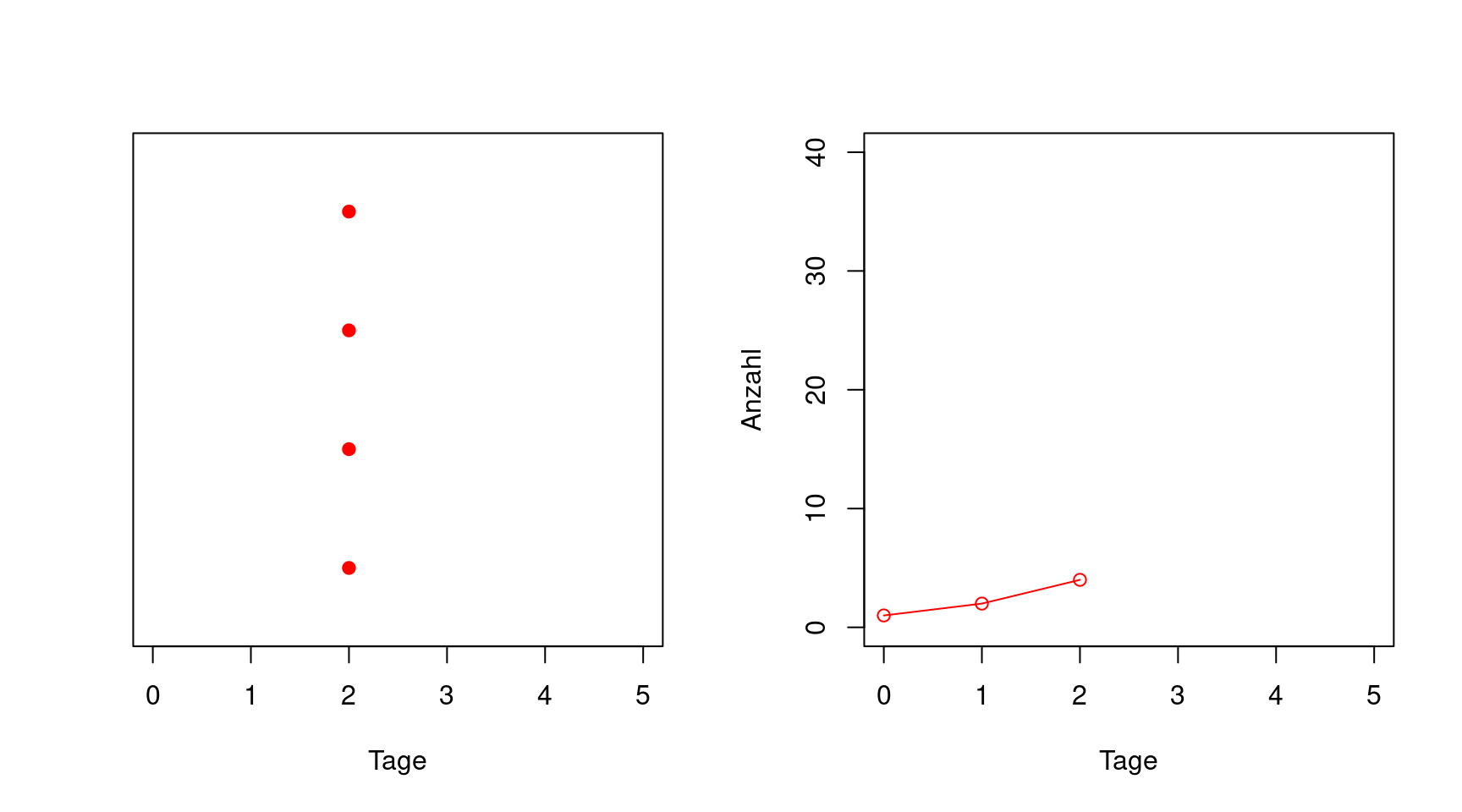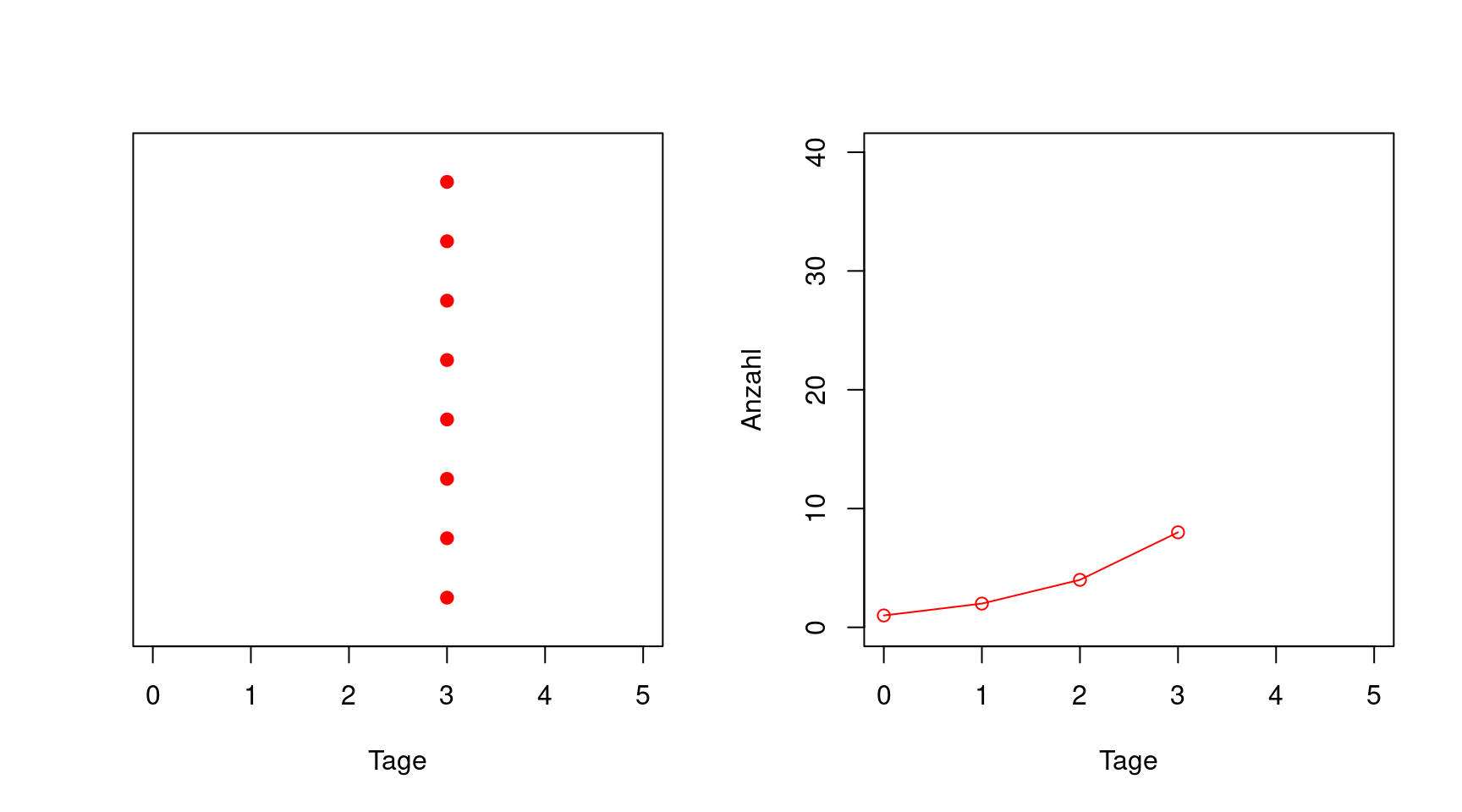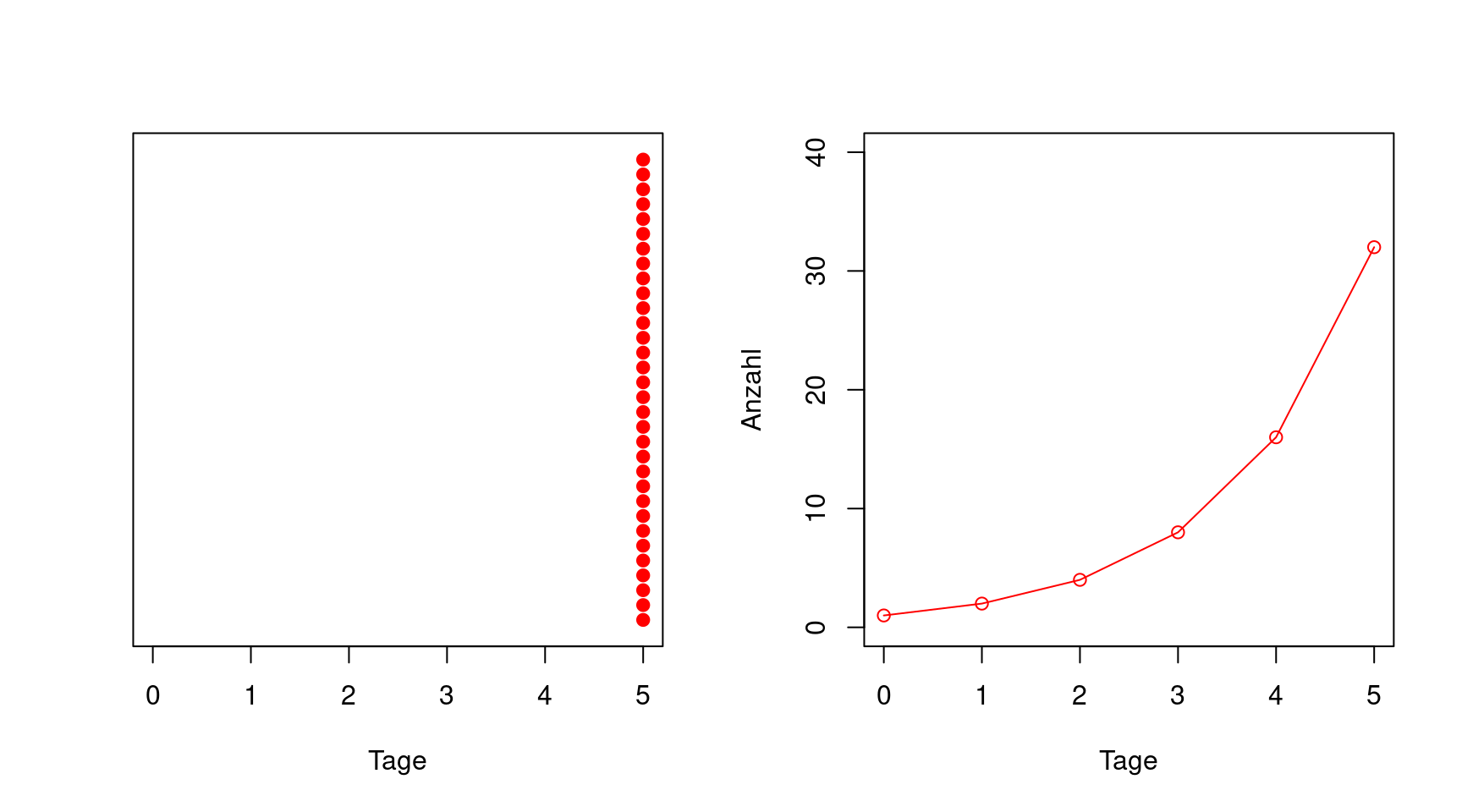
Es ist vielleicht einfacher zu verstehen, wenn der Verlauf visualisiert wird. In der folgenden Animation werden auf der linken Seite die Infizierten als schwarze Punkte dargestellt. Man sieht, dass jeder Infizierte pro Tag einen weiteren ansteckt. An Tag fünf ist es schon schwierig, die Punkte noch auseinanderzuhalten. Im rechten Graphen der Animation wird die Anzahl der Infizierten entsprechend dem linken Graphen in Abhängigkeit vom Tag aufgetragen. Man sieht, dass die Zunahme der Anzahl (die Steigung der Kurve) schnell schneller wird. Genaugenommen verdoppelt sich nicht nur die Anzahl, sondern auch die Steigung jeden Tag.

Logarithmische Abbildung

Wie erkennt man exponentielles Wachstum aus Daten?

Normalerweise benutzt man eine Achseneinteilung in einer Graphik, bei der gleicher Abstand auch gleiche Änderung der aufgetragenen Größe bedeutet, unabhängig davon, bei welchen Werten man sich befindet. Bei einer logartihmischen Skala bedeutet gleicher Abstand immer die gleiche Vervielfachung. Die nächste Abbildung ist identisch zur vorherigen, nur dass in der rechten Graphik die z-Achse logarithmisch ist. Die logarithmische Skala ist so gewählt, dass ein Achsenabschnitt immer einer Verdopplung der darunterliegenden Zahl bedeutet.

Man sieht, dass auf dieser logarithmischen Skala (zur Basis zwei) die gleichen Daten von oben wie eine Gerade aussehen.

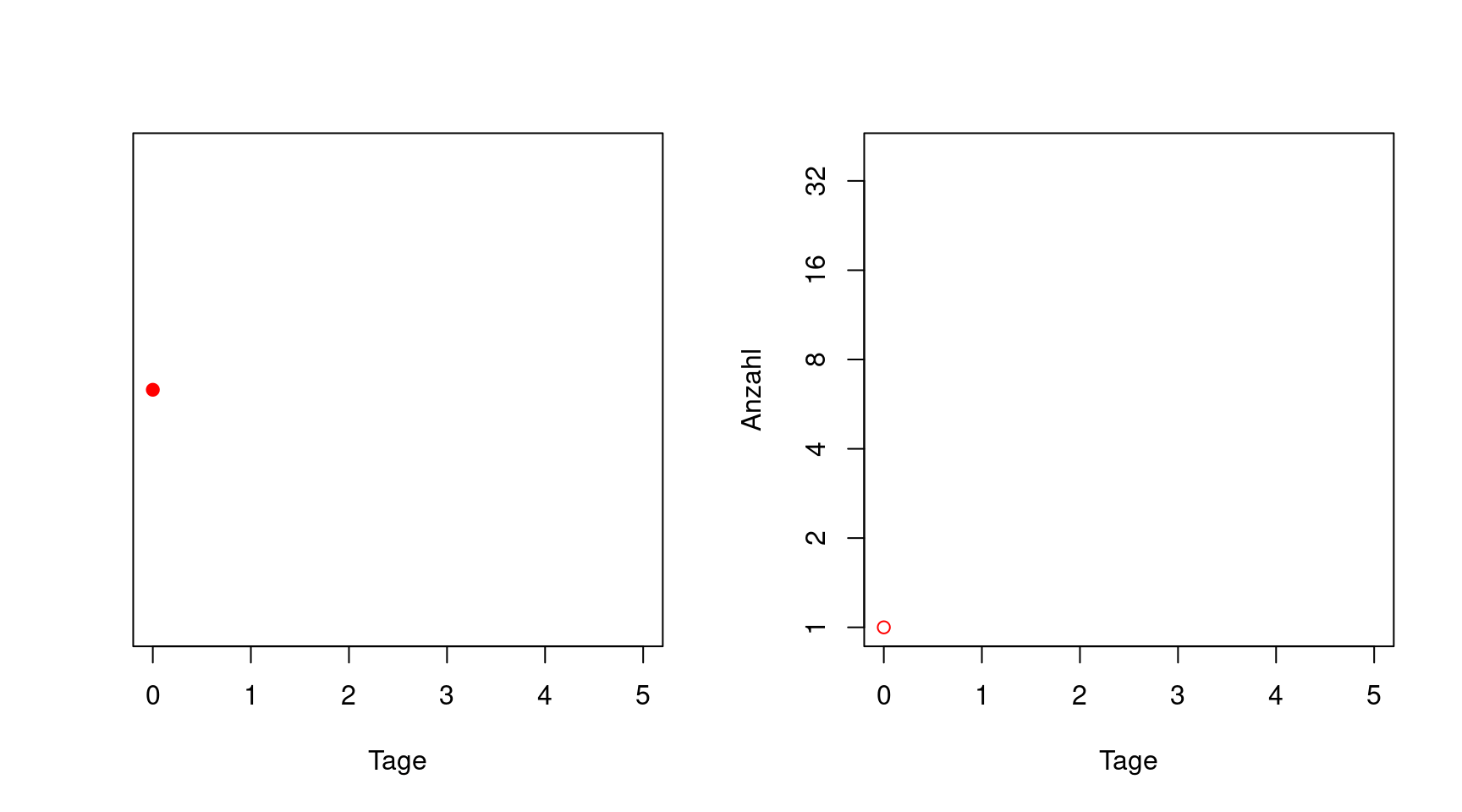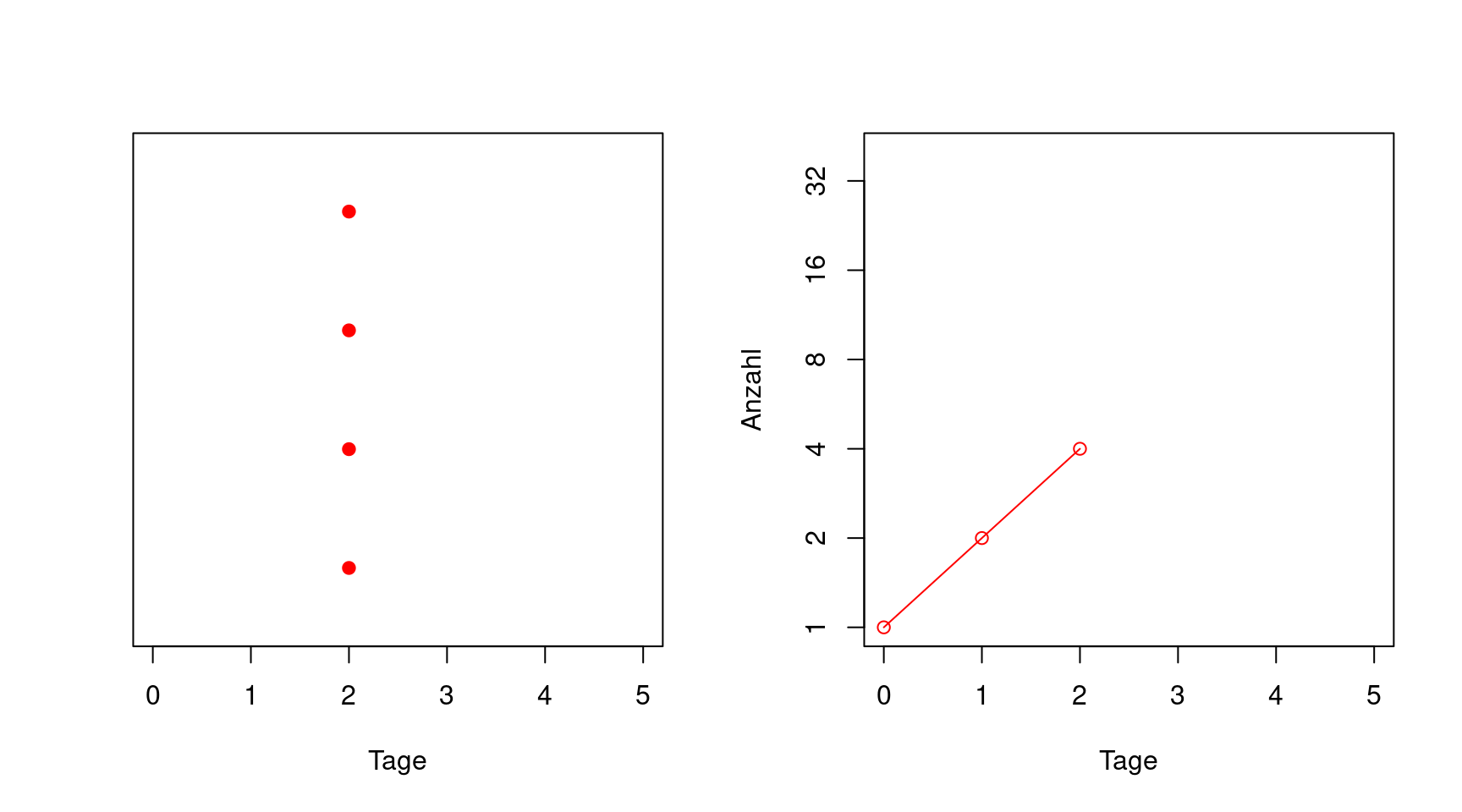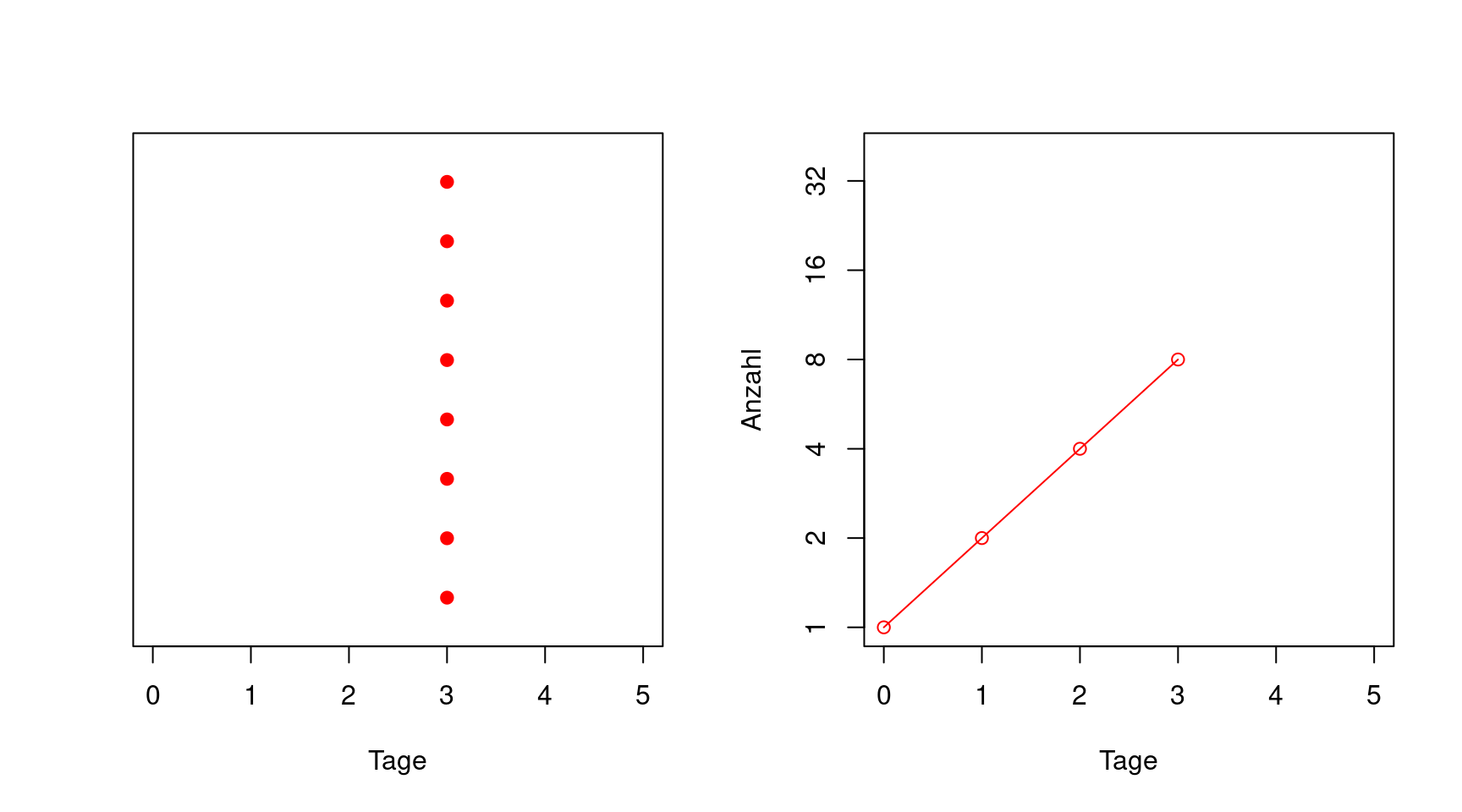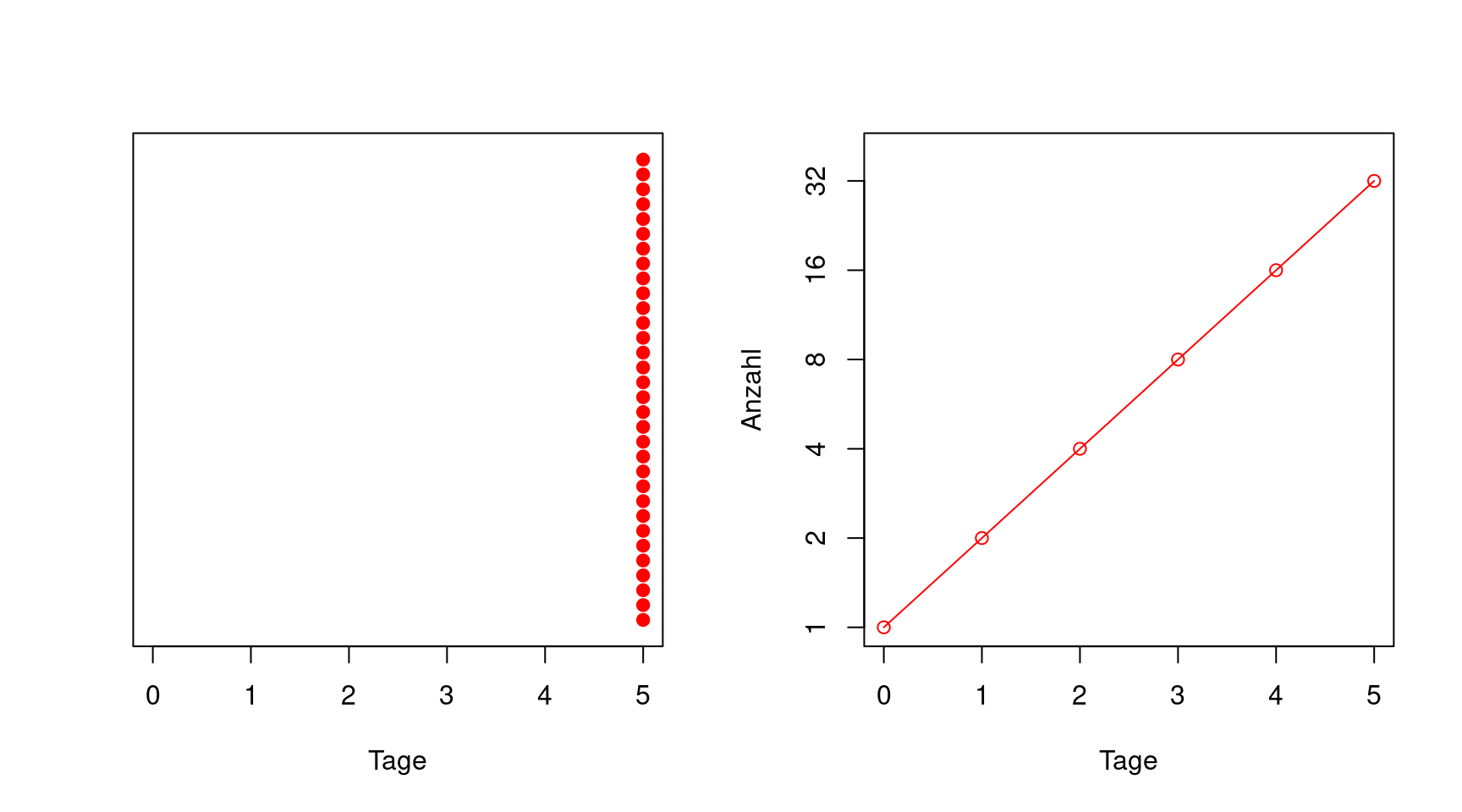
Umgekehrt gilt, wenn man Daten mit einer logarithmischen Skala auf der y-Achse aufträgt und dabei eine Gerade erhält, dann handelt es sich um ein exponentielles Verhalten.

Beispiel

Natürlich ist es im Allgemeinen bei der Ausbreitung von Krankheiten nicht ganz so einfach. Infizierte werden wieder gesund, es werden nicht immer genau gleich viele von jedem Infizierten angesteckt. Außerdem ist ein Population immer endlich, was bedeutet, dass das exponentielle Wachstum nicht ewig weitergehen kann. Das bedeutet einerseits, dass es statistische Fluktuationen auf der Wachstumsrate gibt, und sich die Wachstumsrate außerdem über die Zeit ändern wird, je nachdem in welchem Stadium sich die Ausbreitung befindet.

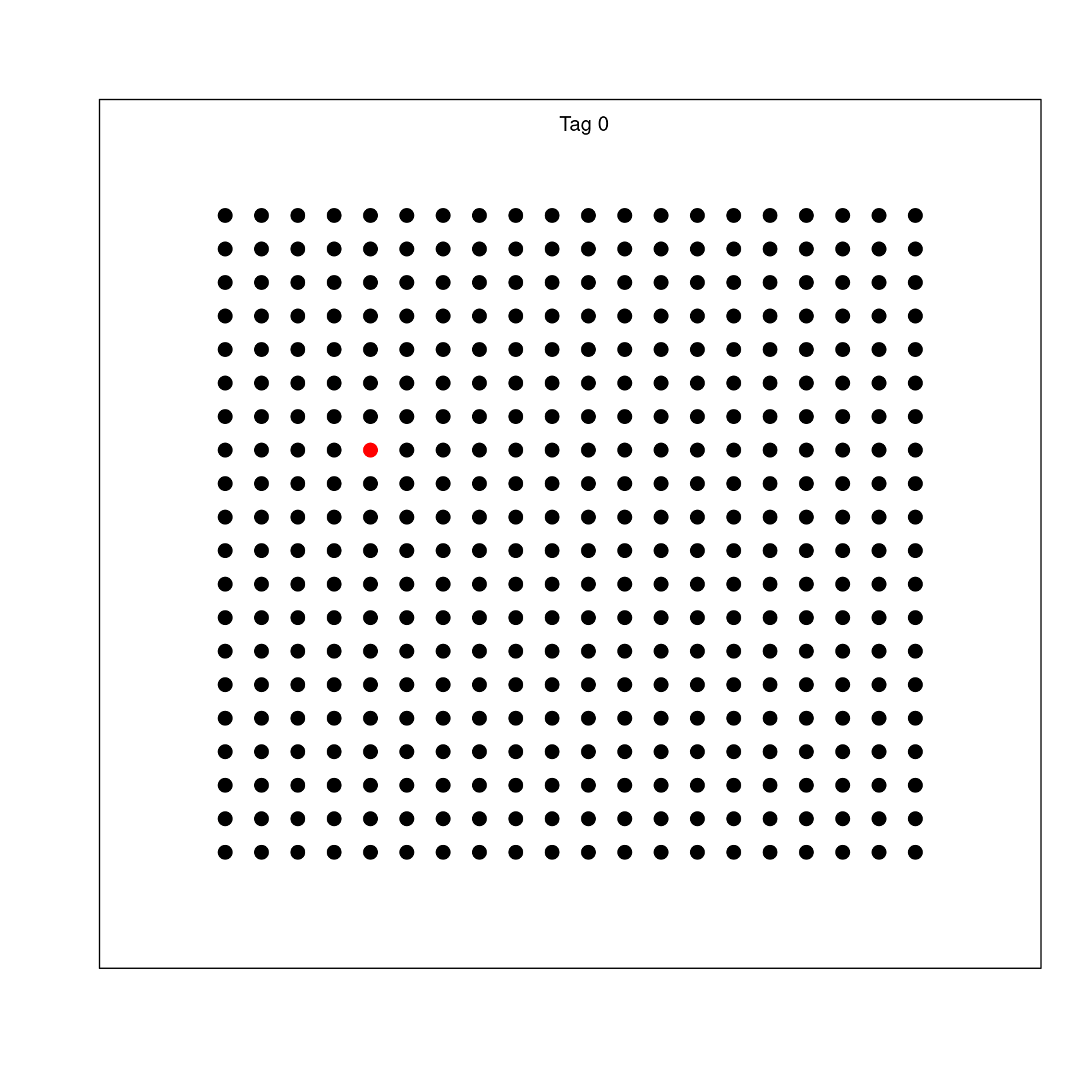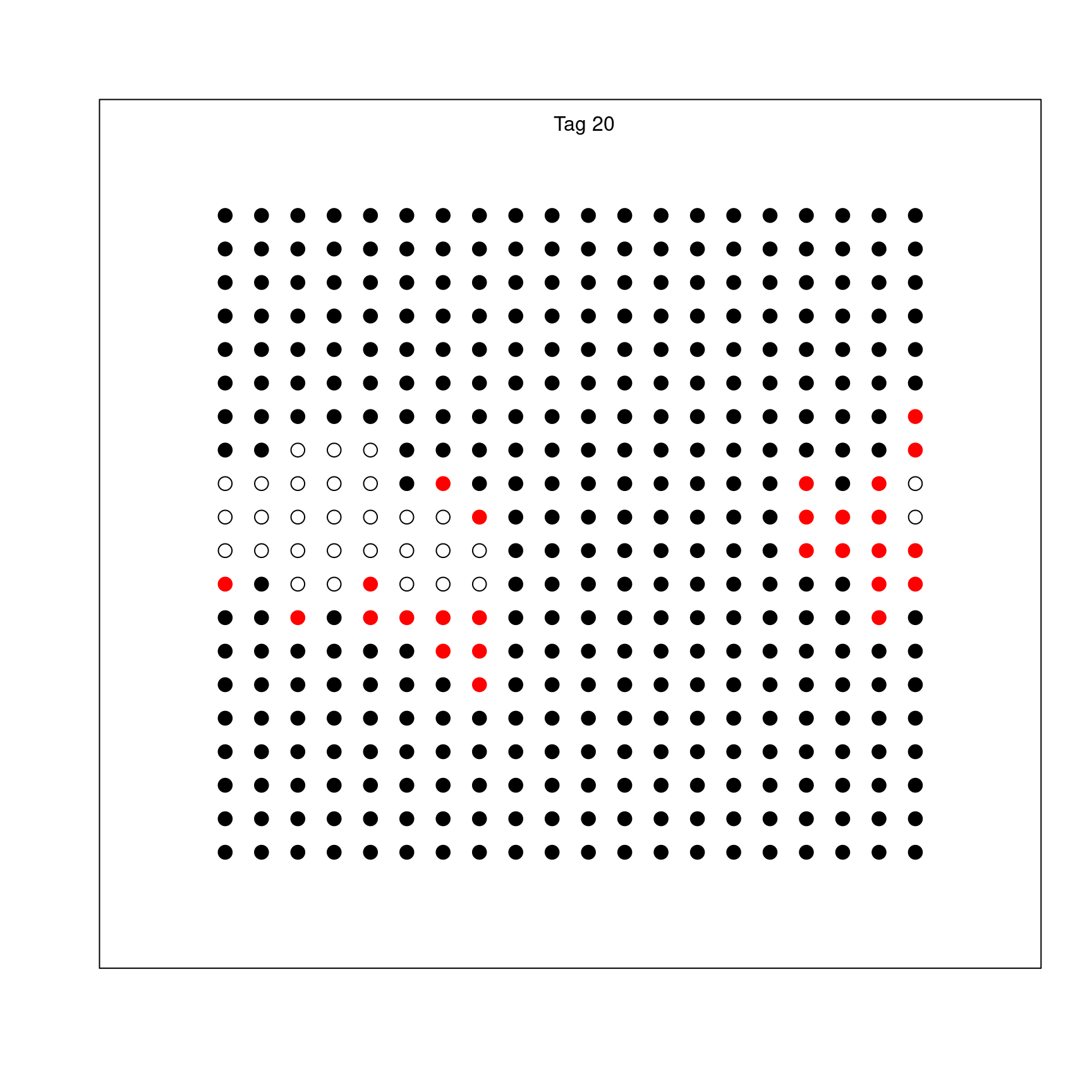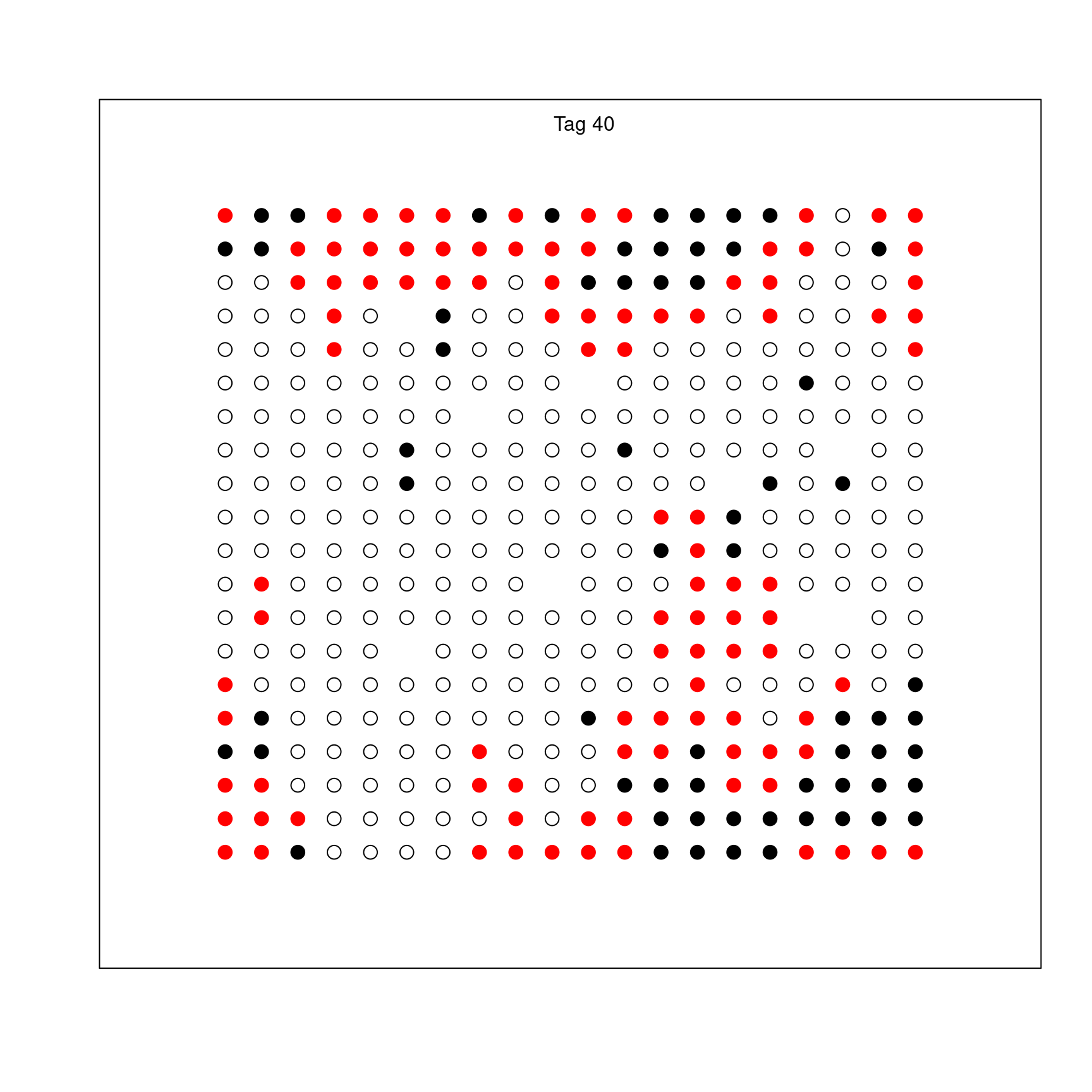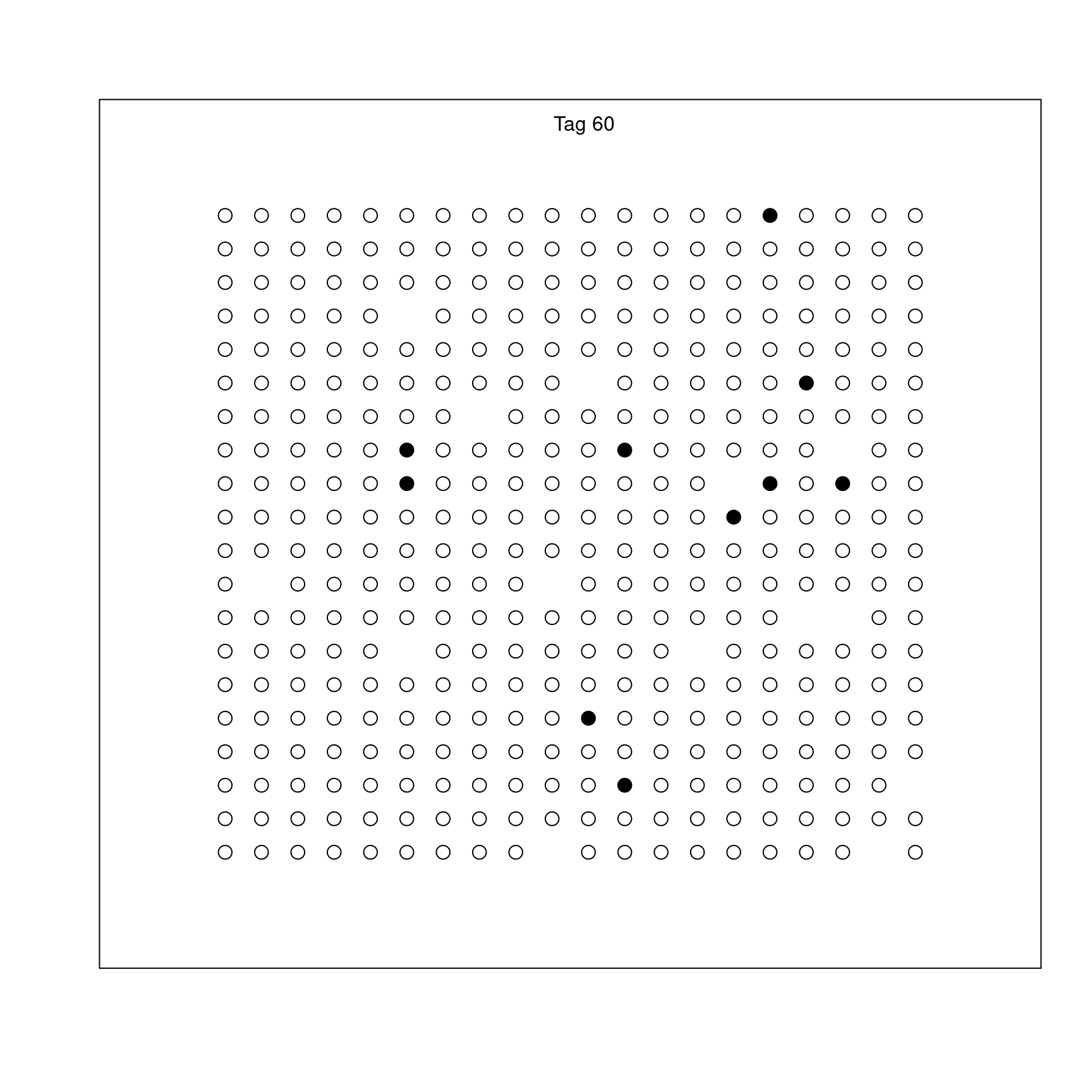
Als Beispiel schauen wir eine Gesellschaft an, die zugegebenermaßen sehr starr ist und nur wenig mit unserer realen Gesellschaft zu tun hat. Es gib 400 Individuen, die jeweils vier Nachbarn haben (oben, unten, rechts, links), mit denen sie Kontakt haben. Am Anfang gibt es einen Infizierten, als gefüllter roter Punkt dargestellt. Noch nicht infizierte sind durch schwarze gefüllte Symbole dargestellt, Genesene und damit immune Personen durch schwarze offene Symbole.

Die Annahmen sind:

Die Krankheit ist 5 Tage ansteckend.
Ein noch nicht Infizierter steckt sich bei einem Infizierten pro Tag mit einer Wahrscheinlichkeit von 19% an.
3% der Erkrankten sterben
Nach der Krankheit sind die Individuen immun.

Ein möglicher Verlauf einer Epidemie ist in der folgenden Animation dargestellt, die ca. 60 Tage dauert..

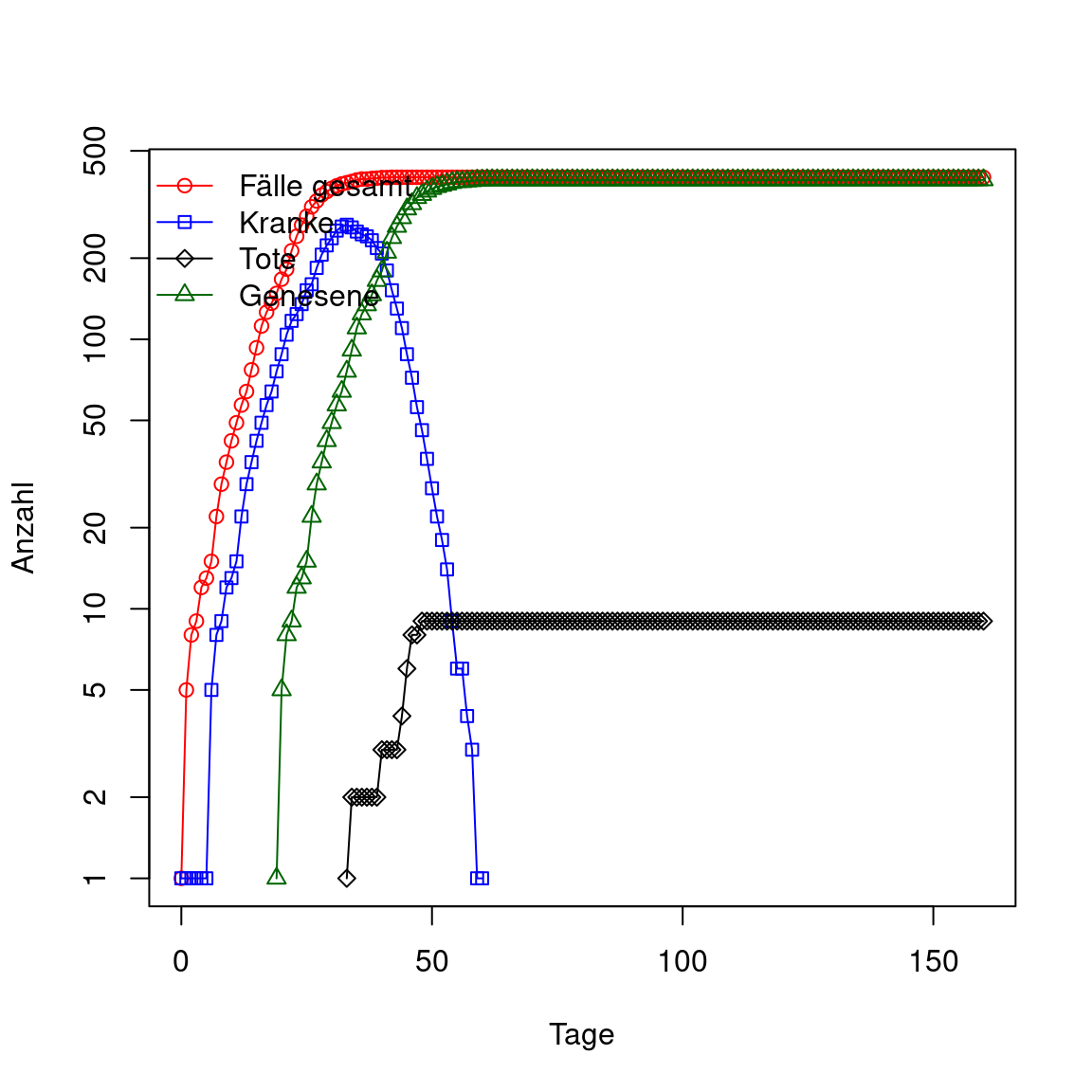
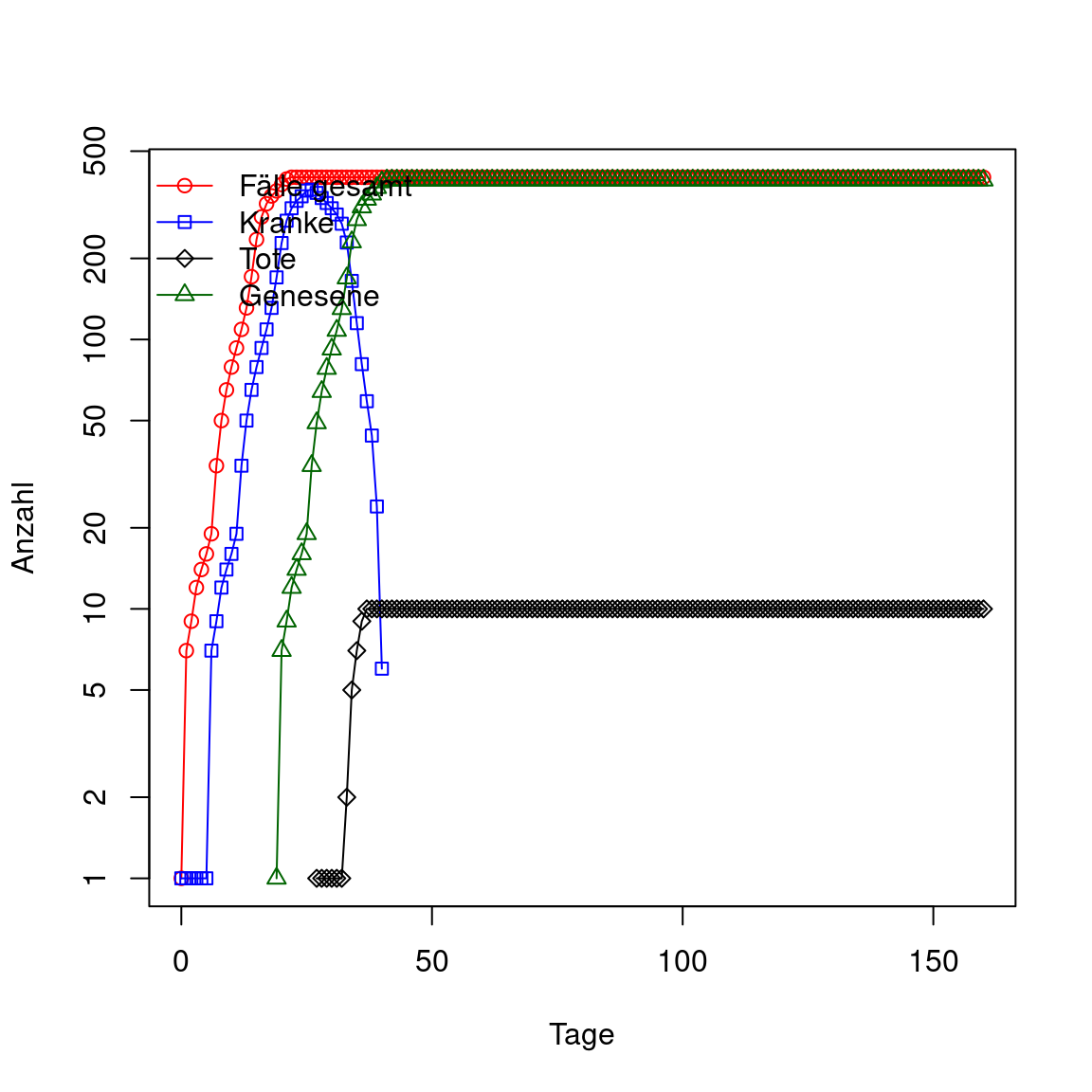
In der folgenden Abbildung wird der Zeitverlauf der Fälle insgesamt, der Kranken, der Genesenen und der Toten dargestellt, mit logarithmischer Skala auf der y-Achse.

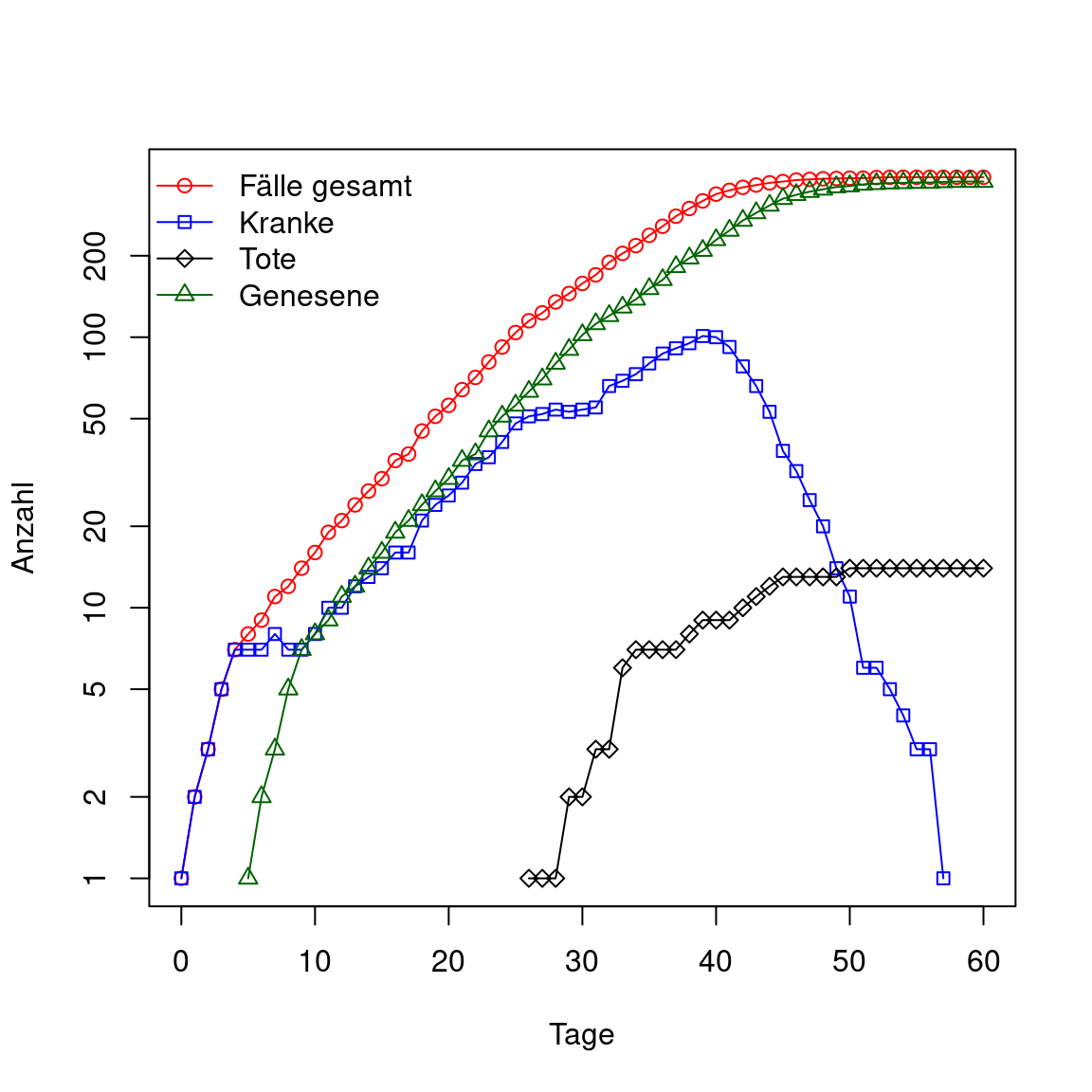
Man sieht einen sehr steilen Anstieg in den Fällen zu beginn von Tag 0 bis 5 ungefähr. Dann flacht die Kurve etwas ab, steigt aber weiterhin exponentiell, aber mit kleinerer Rate, da ab Tag 5 die ersten Individuen genesen und damit nicht mehr ansteckend und auch nicht mehr ansteckbar sind. Eine weitere Änderung der Rate findet um Tag 25 statt: Es gibt jetzt im Mittel weniger ansteckbare Individuen pro Erkranktem, so dass die Rate kleiner wird. Schließlich, um Tag 40 herum flacht die Kurve ab, weil praktisch alle Individuen der Population schon infiziert waren oder sind oder gestorben sind.

Einfluss eines Lockdown

Im Beispiel oben ist praktisch die Gesamte Population einmal infiziert worden. Das liegt an den speziellen und sehr einfachen Verbindungen zwischen den einzelnen Individuen und der Wahrscheinlichkeit, mit der noch gesunde infiziert werden.

Die Idee eines lockdown ist, die Wahrscheinlichkeit für Ansteckung (drastisch) zu reduzieren und damit die Verbreitung zu stoppen bzw. zu verlangsamen. In obigen Beispielmodell können wir natürlich sehr einfach diesen Parameter ändern. Zum Beispiel können wir annehmen, dass ab Tag 15 die Wahrscheinlichkeit von 19% auf 10% sinkt.

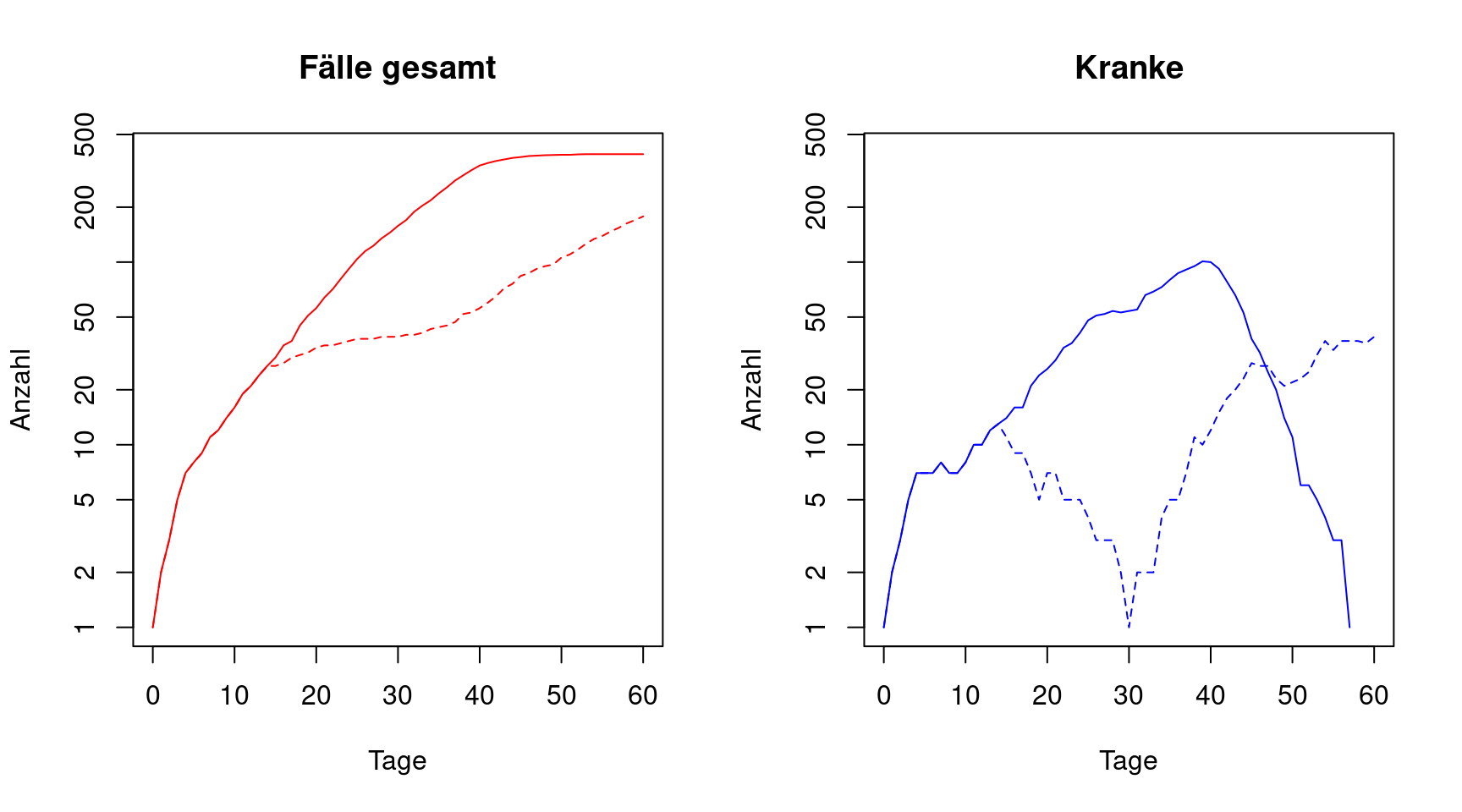
In den folgenden Abbildungen werden die Ergebnisse für das ursprüngliche Modell (durchgezogenen Linien) mit denen eines Modells verglichen, bei dem die Wahrscheinlichkeit ab Tag 15 von 19% auf 10% sinkt.

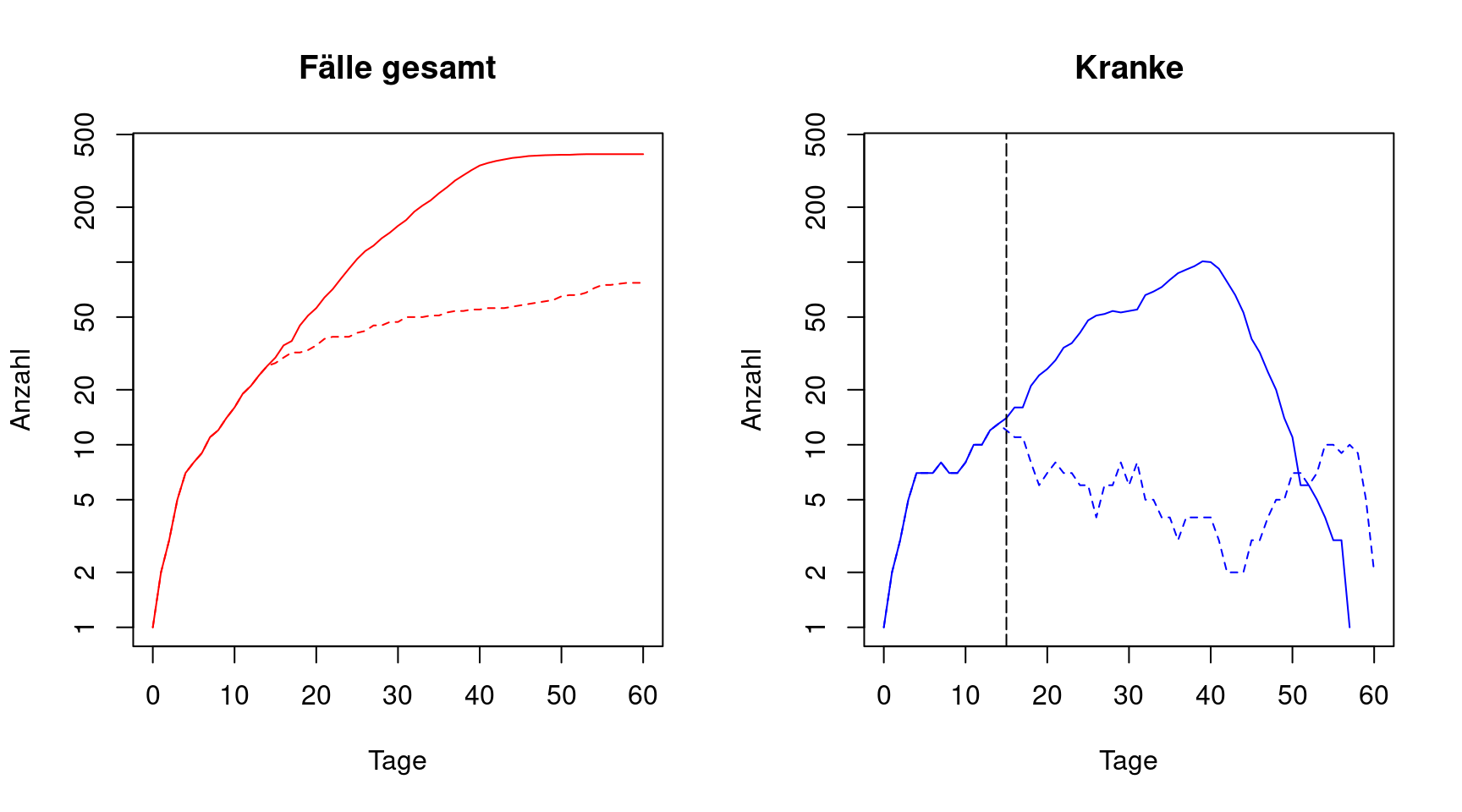
Ab Tag 15 flacht die Kurve der gesamten Fälle erwartungsgemäß deutlich ab. Allerdings wird sie nie ganz flach. Dies erklärt sich damit, dass die Anzahl kranker in den 60 Tagen niemals auf 0 abfällt. Allerdings gibt es maximal 10 Kranke zur selben Zeit anstelle von maximal 100 für das ursprüngliche Modell. Selbst diese Reduktion würde also ein Gesundheitssystem deutlich entlasten, wenn es auch einfach nur deutlich länger dauern würde, bis sich fast alle der Population einmal infiziert haben.

Wenn man die Wahrscheinlichkeit ab Tag 15 noch weiter reduziert, sagen wir auf 5%, so erhält man folgende Bilder:

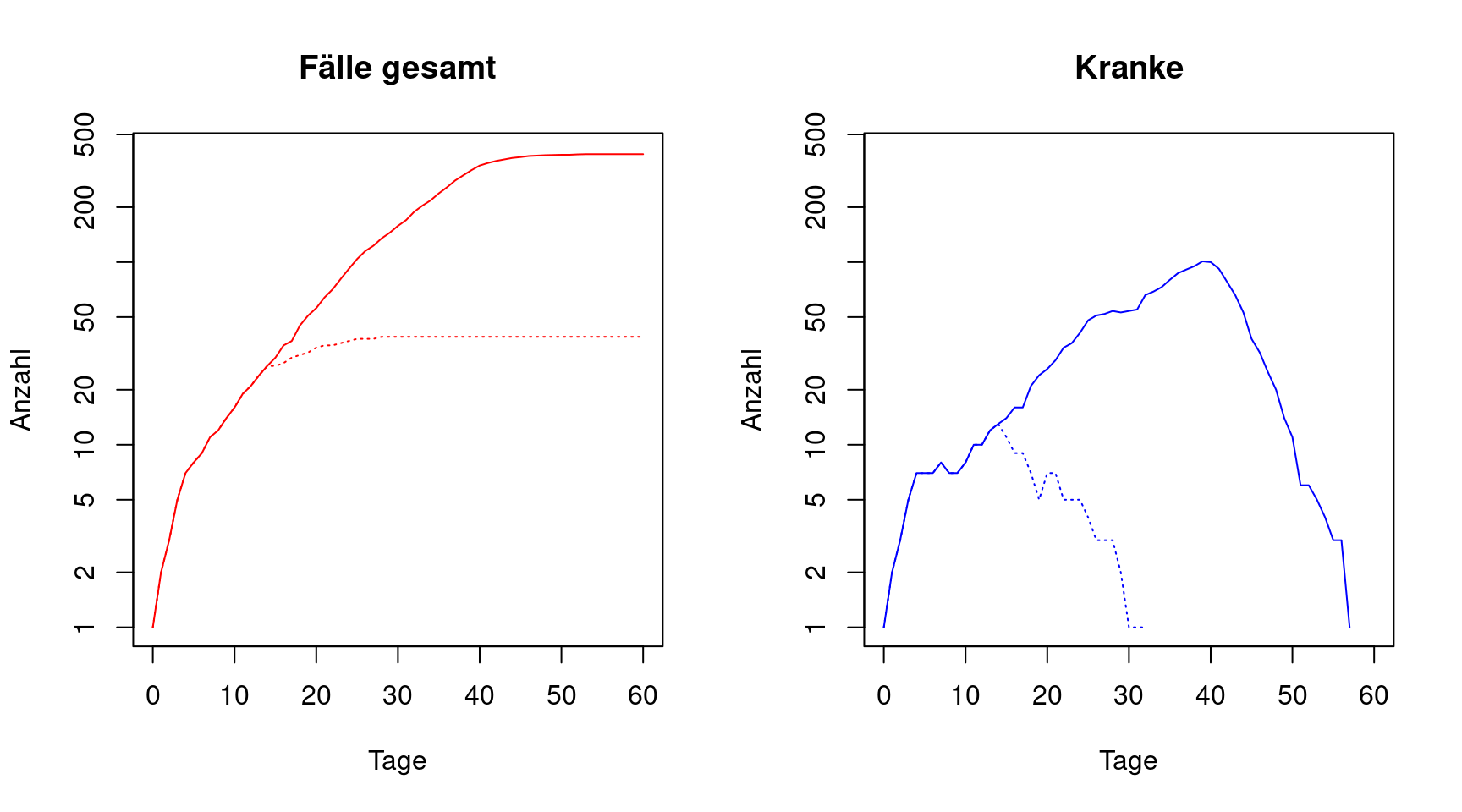
Die gepunktete Linie entspricht dem Model mit 5% Wahrscheinlichkeit für Ansteckung ab Tag 15, verglichen wieder mit dem ursprünglichen Modell. In diesem Fall wird die Asbreitung tatsächlich angehalten und bei Tag 32 beendet.

Auch auf die Todesfälle hat die Änderung der Wahrscheinlichkeit natürlich eine starke Auswirkung, wie in der folgenden Abbildung zu erkenne, in der die drei obigen Modelle verglichen werden: durchgezogene Linie für 19%, gestrichelte Linie 10% und gepunktete Linie für 5% Infektionswahrscheinlichkeit.

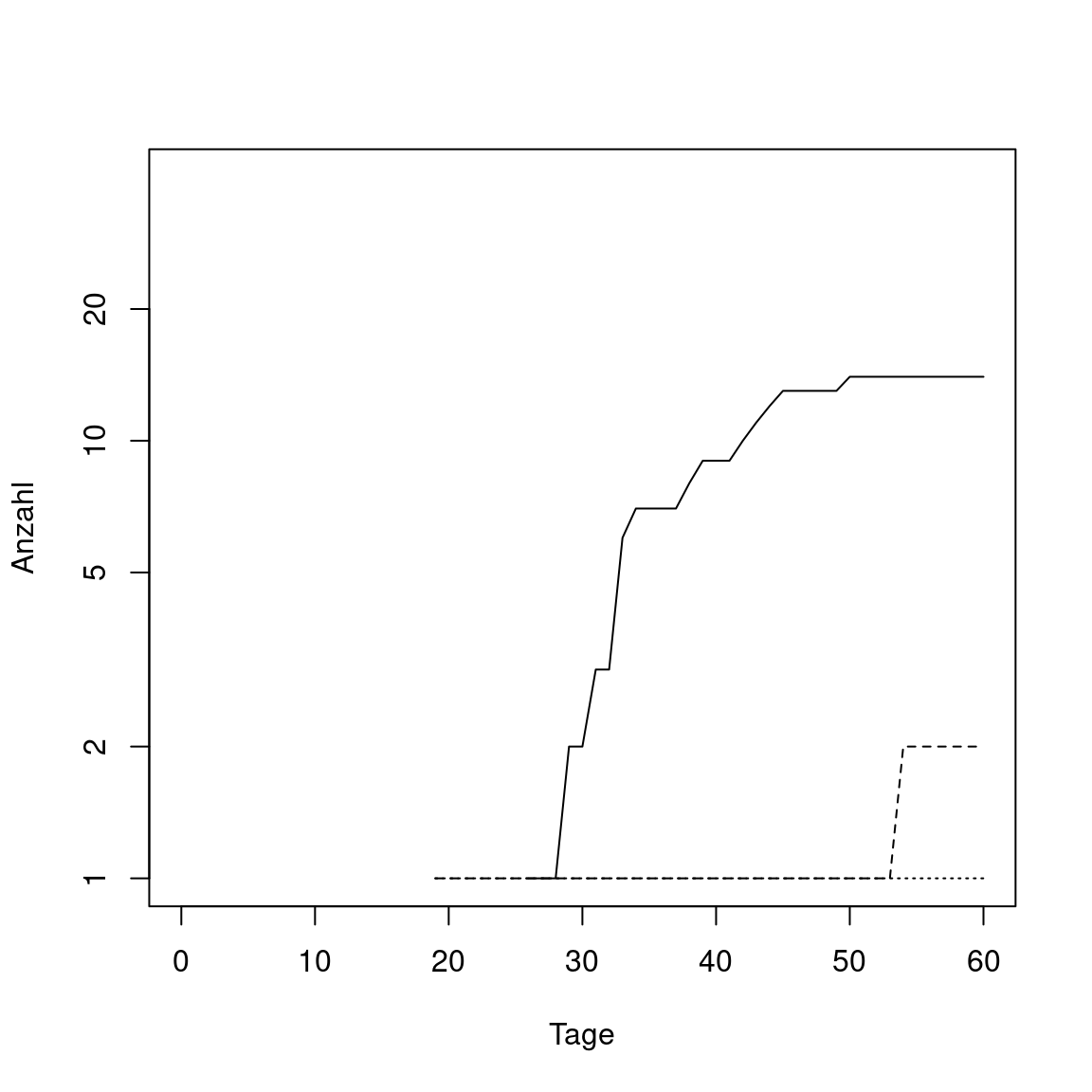
Für den Fall einer strikten Reduktion der Infektionswahrscheinlichkeit auf 5% werden wirklich Leben gerettet. Für die Infektionswahrscheinlichkeit von 10% sieht es zunächst so aus, aber da die Krankheitswelle viel länger dauern wird, als dargestellt, wird es einen ähnliche Anzahl Todesfälle geben, wie für den ursprünglichen Fall.

Hierbei muss man allerdings bedenken, dass das Modell keine Überlastung von Krankenhäusern simuliert, was zu weiteren Todensfällen führen wird. Daher wird auch die Reduktion auf 10% Infektionswahrscheinlichkeit zu einer Rettung von Leben führen, da es nur etwa 10 Kranke gleichzeitig gibt.

… und wenn der Lockdown zu früh aufgehoben wird

In der Realität stellt sich immer die Frage, wann ein Lockdown wieder aufgehoben werden kann und soll. Was passiert, wenn man dies zu früh macht, sieht man in folgender Simulation, in der die Infektionswahrscheinlichkeit erst am Tag 15 auf 5% gesenkt wurde, dann aber am Tag 30 wieder auf 19% steigt. Der eine Kranke am Tag 30 reicht aus, damit die Infektionszahlen wieder exponentiell steigen können.

Trotzdem gewinnt man in diesem Szenario viel Zeit und entlastet ein Gesundheitssystem signifikant. Natürlich hängt es dabei wieder kritsch davon ab, wann der Lockdown aufgehoben wird.

Ein realistischeres Netzwerk

Das quadratische Gitter mit periodischen Randbedingungen von oben ist natürlich sehr unrealistisch. Eine Gesellschaft kann realistischer durch sogenannte small world Netzwerke abgebildet werden. Als Beispiel nutze ich hier entweder ein Watts–Strogatz small world Modell oder ein Barabási-Albert-Modell.

Zunächst das Watts–Strogatz Modell:

library(igraph)

## 
## Attaching package: 'igraph'

## The following objects are masked from 'package:stats':
## 
##     decompose, spectrum

## The following object is masked from 'package:base':
## 
##     union

set.seed(9)
dim <- 2
n0 <- 20
## a small world network with 40000 nodes
g <- sample_smallworld(dim=dim, size=n0, nei=3, p=0.05)
p <- 0.01

Die Anzahl der Knoten beträgt \(400\) Knoten.

Nun das Barabási-Albert-Modell: